前馈神经网络
前言
从这一节就开始接触最简单最朴素的神经网络了,叫做前馈神经网络。在这种神经网络中,各神经元从输入层开始,接收前一级输入,并输入到下一级,直至输出层。整个网络中无反馈,可用一个有向无环图表示。
通常我们说的前馈神经网络有两种:反向传播网络(BP网络)和径向基函数神经网络(RBF网络)。
这一节虽然不难,但是非常重要,因为几乎所有在深度学习中涉及的最为关键性的问题都在这一节涵盖了。我们以最简单的BP网络为例,看看最简单的神经网络是怎么设计和工作的。
本节目录:
- 线性回归的训练
- 神经网络的训练
- 小结
线性回归的训练
也就是之前讲过的线性函数:y=wx+b ,在拟合的过程中,我们添加一个参数 e 代表 error,表示误差的含义,于是就有了:y=wx+b+e
当取定每一个 w 和 b 的时候,只要带入一个 x 和对应的 y 就一定会产生一个 e 来表示这个误差。所以总的误差就可以表示为:
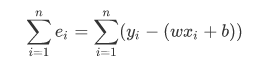
但是显然也是有一个问题的:这种误差能内部正负相互抵消的吗?显然是不能的。所以我们取其平方和,即:
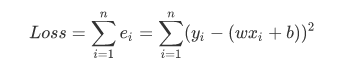
在完全展开之后,在合并公因式以及常数项之后,得到类似以下形式:
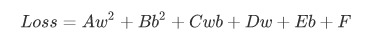
A - F 都是常数系数,现在我们得到了一个全局的误差函数,其中未知数是 w 和 b。现在我们要做的就是找到一对 w 和 b 使得Loss 误差值越小越好。
这你估计就坐不住了,求导求最小值嘛,高中我就会。事实上的确是这样,这里介绍一种很开阔思维的算法:梯度下降法。
还是以最简单的说起,假如求 y=f(x)=x^2 + 1 的最小值:
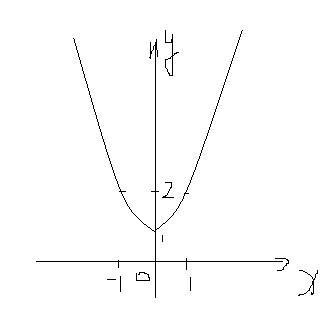
聪明的你一眼能看出来极值在哪,但是计算机就比较笨了,它只能先选取一个点,比如是(1,2),选中之后往左挪发现值比它小,往右挪发现值比它大,所以它肯定会往左挪来让自己变得小,也就越接近极值。但是我们希望它能够在离极值点远的地方挪动的幅度大一点,在极值点近的地方挪动的幅度小一点,这该怎么办呢?这就是梯度下降法要解决的问题。
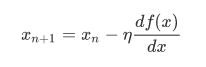
这表示的是一个更新逻辑过程,X(n+1) 和 X(n) 分别表示两个临近迭代中的 x 值,X(n+1)是X(n)更新后的下一次迭代的值,每次更新都把后面的值赋值给前面,其中的希腊字母称为学习率,也就是一个挪动步长的基数,在学习伊始由编程人员赋值进去就好了。至于为什么这样写?自己仔细想想就明白了。
所以,对于像上面的凸函数(从函数图像下方往上看),用梯度下降法的核心思路就是:在函数的曲线(曲面)上初始化一个点,然后让他沿着梯度下降的方向移动,直至移动到极值的位置。
那对于多元函数该怎么办呢?直接上答案了:
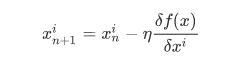
就是把导数变为偏导数。
神经网络的训练
隐藏层:
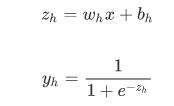
输出层:
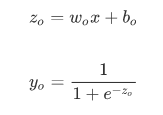
那么损失函数也就可以定义为:
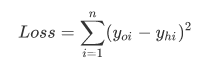
其实线性模型我们已经搞定了,就是挪啊挪找极值,而对于激励函数依旧是这样。
准备样本
这个要注意的是,如果要做图片分类的话,还要为每个样本打上标签,如果这里只是用数字作为样本,有输入和输出就行了。
清洗处理
这个过程是比较复杂的,也是整个神经网络和深度学习中比较难的地方。处理的目的就是为了帮助网络更高效、更准确的做好分类。
正式训练
然后就是代入样本开始训练,找到让损失函数值最小的待定系数。
小结
到这里,我们已经了解了一个简单的神经网络训练过程和原理,后面我们还会见到很多构建复杂的神经网络,从本质上讲,都是通过不断调整各个神经元中待定系数使得损失函数向不断降低的方向移动。
注意,在实际生产环境中,可能会遇到更加糟糕的损失函数,它不是凹凸函数,可能是坑坑洼洼的形状,则要求所有极小值点进行比较了,当然,TensorFlow已经封装了这些东西。
