从零开始认知深度学习
前言
上一节我们学了机器学习相关的知识,感觉还是蛮好理解的,也很有意思。这节就开始认识一下深度学习了。这一节也是偏重于理论知识,理解起来也很简单。对了,push上去的时候,发现网页并没有解析MarkDown里面的数据表达式,这就很僵了。
对于上一篇可见:从零开始认知机器学习
图片一个一个截的,蛮麻烦的。之后可能就不截图了,反正也没人看。
提供下载:从零开始认知机器学习
我尽可能的把写完的放在服务器上吧。
本节目录如下:
- 神经网络是什么?
- 神经元
- 激励函数
- 神经网络
- 深度神经网络
- 深度学习为什么这么强?
- 不用再提取特征
- 处理线性不可分
- 小结
神经网络是什么?
要讲深度学习之前,就一定要了解神经网络。人们想出深度学习实现方式的思路就是来源于神经细胞之间传递信息的方式。下面,我们就开始了解一下神经网络的最基本的组成单元 —- 神经元。
神经元
最简单的神经元就是有一个输入,一个输出。不过,我们现在使用的神经元有两部分组成:线性模型和激励函数(又叫激活函数)。
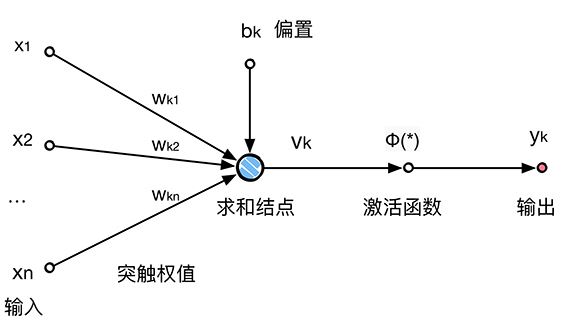
从输入到求和结点就是之前讲的 f(x)=wx+b 的过程。从图中也可以看出,x 是一个 1xn 的矩阵向量,w 是一个 nx1 的矩阵,表示权重值,而 b 表示偏置值。
激励函数
Sigmoid 函数
之前就见过这个函数,即:
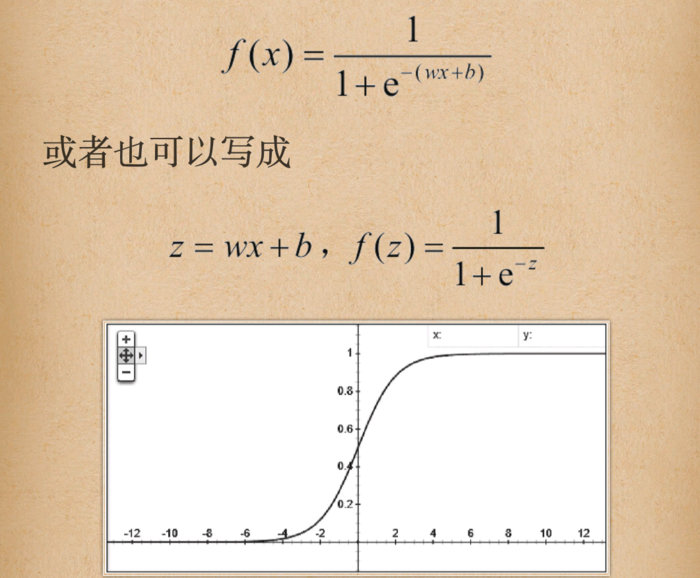
其中 z = wx + b ,也就是线性模型。
激励值最终投射到 0 或 1 两个值上,而其他输出值纠就介于两者之间,表示激活程度不同。
Tanh 函数
也应该算是比较常见的激励函数了,后面学习循环神经网络RNN就会接触到了。
Tanh函数也叫双曲正切函数,表达式如下:
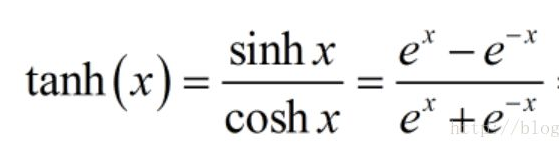
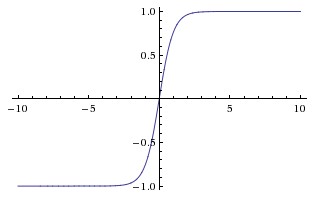
可以看到Sigmoid 函数和Tanh函数很像,Sigmoid 在|x|> 4 趋近于 0 或 1 ,而Tanh函数在|x|>2 趋近于 -1 或 1。
RelU函数
RelU函数是目前大部分卷积神经网络CNN中喜欢使用的激励函数。
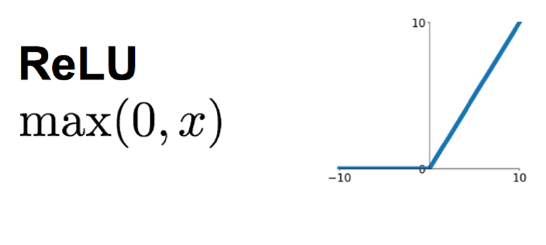
这个函数的形式:y=max(0,x) 在原点左侧斜率为0,右侧斜率为1。
神经网络
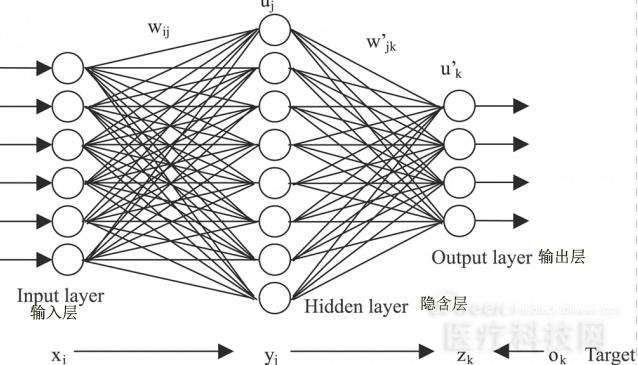
在一个神经网络中通常会分为三层:输入层、隐含层和输出层。
输入层在整个网络的最前端位置,直接接受输入的向量,不对数据做任何处理,通常这一层是不计入层数的。隐含层可以有一层或者多层,输出层是最后一层,用来输出整个网络处理的值。
深度神经网络
深度学习实际上是基于深度神经网络的学习,称为 Deep Learning,Deep也就是指神经网络的深度,当然,也没有明确表示大于多少层算作深度。
这里需要注意一点,就是深度学习不是在任何情况下都要比传统的机器学习表现更好。传统机器学习在工作的过程中具有很好的解释特性,或者说你知道模型在做什么,处理的是什么特征,其中的任何一个指标值的大小变化的意义都会有良好的解释。而且,传统机器学习在训练的过程中需要很少的样本向量,通常都是百级或者千级就够了,这对于深度学习来说也是无法做到的 —- 它需要数以万计的样本来做训练,所以,我们不能盲目的迷信深度学习的能力,也不能误读深度学习的作用。
深度学习为什么这么强?
神经网络,尤其是深度神经网络之所以这么吸引人,主要是它能够通过大量的线性分类器和非线性分类器的组合来完成平时非常棘手的线性不可分的问题。
不用再提取特征
前面我们说过,在传统的机器学习中,使用决策树、支持向量机SVM这些分类器模型中,提取特征是一个非常重要的前置工作,也就是人类在驱使这些分类器开始训练之前,就要把大量的样本数据整理出来,“干干净净”地提取其中能够清晰量化的数据维度,否则,这些基于概率和空间距离的线性分类器是没办法进行工作的。
然而在神经网络中,由于巨量的线性分类器的堆叠以及卷积网络的使用,它对噪声的忍耐能力、对多渠道数据上投射出来的不同特征偏向的敏感程度会自动重视或者忽略。这样,我们在处理的时候,人类所需要使用的技巧就没有那么高要求了,也就是我们通常所说的 End - to -End 的训练方式。
处理线性不可分
神经网络还有一个最神奇的地方,那就是用大量的线性分类器的堆叠使得整个模型可以将线性不可分变得可分。神经网络的每一个神经元都是一个线性分类器,所以神经网络能且通过线性分类器的组合来实现线性不可分问题。
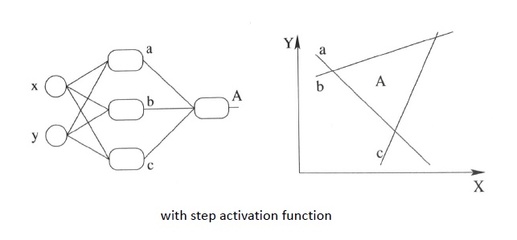
例如:对于平面中的一个三角形 A ,如果我们想用一条线(一个线性分类器)把它分开,显然是做不到的。但是我们可以通过画三条线,也就是图中对于的 a、b、c 把三角形分离出去。也就是说要同时满足四个分类器的一个分类标准才算是我们要约束的一个分类,也就如图左示,构造这样一个模型。
小结
理解一个基本的神经网络构造也不是什么难事,深度学习前景广阔,一个“摸不到天花板”的领域,需要学习的知识太多了,努力加油!
